I am generally all for not legislating anything, but the world really does need to use a commonly agreed system for physical measurements. That system is, like it or not, metric. Or rather SI units. I am sure I am not alone in thinking that some mistakes were made in the SI unit system — particularly in the selection of the fundamental units (kilograms? FFS, why not have made the base unit unmodified?). Metres aren’t a particularly convenient human size — feet are, inches are, that’s why they persist. Worrying about the actual sizes misses the point though. The point of SI units is that it they are consistent, repeatable and scalable.
Let’s consider length.
- A nanometre is a thousandth of a micrometre
- A micrometre is a thousandth of a millimetre
- A millimetre is a thousandth of a metre
- A metre is a thousandth of a kilometre
- A kilometre is a thousandth of a megametre (although this is outside human daily experience, so we don’t hear this said a lot).
You can see these are all “metresâ€, just scaled up or down by a factor. The particular factor used is indicated by one of the SI prefixes.
The factor “a thousandth†is convenient for humans, we can hold a times one thousandth scale in our heads (think of a metre-rule, focus in on one centimetre of it and imagine a tenth of that centimetre — you can do that without much trouble and it’s a scale that is within our experience to understand). Typically engineers like to keep to these “thousandth†factors: nano, micro, milli, kilo, mega, giga, tera — but a few inbetween ones for hundredths and tenths don’t cause any trouble, centi, deci, deca, hecto. What’s more once you’ve learned to use the prefixes with metres, you have no trouble with terawatts, gigabytes, microseconds, or decibels.
Now in imperial.
- A mil/thou is a thousandth of an inch
- An inch is a twelfth of a foot
- A foot is a third of a yard
- A yard is 1760th of a mile
WTF? The factors between units are essentially random, and they don’t carry to other units. Throw in a few more, still in use in the US.
- A link is one twenty fifth of a rod
- A rod is one quarter of a chain
- A chain is one tenth of a furlong
- A furlong is one eighth of a mile
Double WTF? When you’re in an argument with someone about the advantage of imperial units, simply ask them “how many millimetres are there in a kilometre? How many inches are there in a furlong?â€. It doesn’t matter whether they know it or not; the point is that you’ve got far more chance of understanding/calculating that a millimetre is a millionth of a kilometre than you have of knowing that an inch is one 7920th of a furlong.
There are seven SI base units; unless you studied physics you probably aren’t aware that every single other unit can be defined in terms of the base units (being chosen as a base unit doesn’t actually imply that the universe “sees†them as base, all units can be defined in terms of other units, we’ve just picked a convenient set of seven that represent physical quantities that cannot be defined in terms of each other — they are an orthogonal set).
The measure of capacitance, the Farad, is actually a seconds-to-the-forth-power amperes-squared per kilogram per square metre. You can see why we give it a shorter name. Have a shot at defining it in Imperial units… no?
You see? The fact that a pint is more convenient day-to-day than a litre is not the point; what is the point is that a litre is a thousand millilitres, and a millilitre is one cubic centimetre and one cubic centimetre of water weighs one gram (I could moan about the silly definition of a litre, but at least it is in terms of SI units). A pint is … well, it’s not defined in terms of anything, it just is. Until we got SI units, there was no way of giving a precise size to pint — evidenced by the fact that across Europe it varied from around half a litre to a litre.
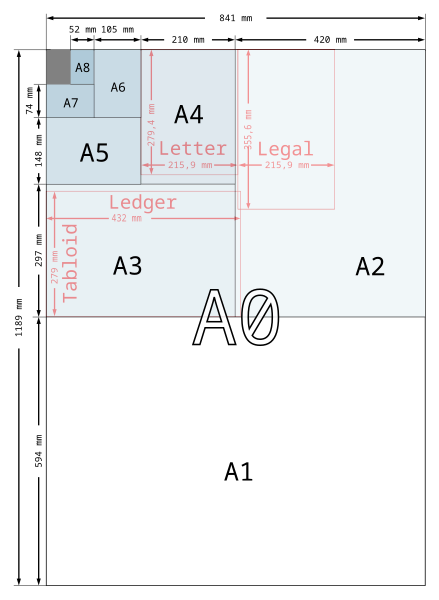
While I’m on standards, let’s talk paper sizes. Fortunately, there hasn’t been much difficulty in getting people to accept the standard ISO paper sizes in the UK. Again it’s only the crazy Americans who refuse to see sense. You might not know why they’re so good. I’ll tell you.
Get some sheets of A4. Put one sheet next to the other. You now have A3. Make another virtual sheet of A3. Put it next to the first A3. You now have A2. Again, A1. Again, A0.
4i
That sheet of A0 has an area of one square metre. Have a look at the packet you got your paper from. It probably says 80 g/sqm. Therefore the weight of A0 is 80g. The weight of A1 (being half the area of A0) is 40g. A2 is 20g; A3 is 10g; A4 is 5g. Count how many pages of A4 you are sending — multiply by 5g. Now you know what stamps to put on, and you haven’t had to use a scale.
Take two sheets of A4. Put them in a photocopier. Set the photocopier to reduce to 70% (
). Your two sheets of A4 (effectively A3) have been shrunk to A5 size each, and fit 100% on a sheet of A4.
This trick works because the ratio of the long side to the short side is defined as the square root of two. It is the same ratio regardless of which A series paper you pick.
If you can, grab a piece of American letter or legal paper. Or perhaps a book that uses a non-ISO page size (books have a different set of problems, but there are ISO standards; unfortunately few use them). Try the same tricks as described above (anyone who has tried to photocopy facing pages of a book will understand that it doesn’t work well); weep as you do so. Pity our American cousins, who suffer with utterly dreadful paper.
The B-series and C-series follow the same rule: the ratio of the sides is
. Of course you can pick any base size you want and create a series with that rule. Each of the series provides a different condition for the base size.
- A-series. A0 is one square metre.
- B-series. B1’s area is the geometric mean of A0 and A1 (i.e.
. It provides in-between sizes that the A-series doesn’t — posters and passports.
- C-series. C0’s area is the geometric mean of A0 and B0. The C-series provides sizes that are “a litle bit bigger†than one of the A or B series. It’s used for envelopes. An A4 letter fits inside a C4 envelope.
Hopefully you’re convinced that metric measurement is good; and ISO paper is really clever.